The Self-Similar Rayleigh-Gans Approximation
The Self-Similar Rayleigh-Gans Approximation (SSRGA) provides a
means to compute the scattering properties of aggregated ice
particles and snowflakes in the microwave and millimetre parts of
the spectrum. In this regime the soft sphere/spheroid approximation
tends to significantly underestimate scattering, while the Discrete
Dipole Approximation (DDA) is very computationally costly. The SSRGA
is a fast method that computes the ensemble average scattering
properties of aggregate particles and which matches DDA calculations
well in the case of unrimed particles. It combines two assumptions:
- Rayleigh-Gans Approximation: the electric field within the
particle can be approximated by the incident field, valid if the
effective dielectric constant on the scale of the wavelength is
close to one. This is also known as the Born approximation.
- Self-Similar Approximation: the process of aggregation
leads to the particle having an internal structure that is fractal
in nature and can be described by a power law, found to be valid for
ice aggregates simulated by two completely different aggregation
models. For particles larger than the wavelength, it
turns out that the internal structure of ice particles is crucial
for determining their scattering properties.
The theory has been developed in two papers:
- Hogan
and Westbrook (2014) derived the SSRGA equation for radar
backscatter and fitted the three SSRGA parameters to aggregates
generated by Westbrook's aggregation model. (Hogan, R. J., and
C. D. Westbrook, 2014: Equation for the microwave backscatter cross
section of aggregate snowflakes using the Self-Similar Rayleigh-Gans
Approximation. J. Atmos. Sci., 71, 3292-3301)
- Hogan
et al. (2017) extended the method to derive the scattering
and absorption cross-sections and the full phase function. They
showed how the Rayleigh-Gans Approximation should be modified to
account for the enhanced backscatter and absorption by
non-spherical monomers, and tested the revised method using DDA
calculations performed on aggregates simulated by two different
models. (Hogan, R. J., R. Honeyager, J. Tyynela and S. Kneifel,
2017: Calculating the millimetre-wave scattering phase function
of snowflakes using the Self-Similar Rayleigh-Gans
Approximation. Q. J. R. Meteorol. Soc., in press)
See also
a talk
presented at the AMS 14th Conference on Atmospheric Radiation,
Boston, 7 July 2014.

Example of a simulated aggregate of bullet rosettes from the
model of Westbrook et al. (2004), shown in the plane of its
longest (x) dimension and shortest (z) dimension, with the
intensity of the shading proportional to the amount of ice in the
third (y) dimension. Simulations such as these were used to
demonstrate the self-similar nature of the struture of
aggregates. Taken from
Hogan
and Westbrook (2014).
Download
- scatter-1.1.tar.gz (12 Oct 2019):
A program to generate particle scattering properties (in the form of
NetCDF files) for use in cloud, aerosol and precipitation retrieval
algorithms from active and passive sensors. It includes the SSRGA
algorithm as well as Mie theory and the T-matrix method. It is
written a mixture of C and Fortran and is released under the terms
of the Apache License, Version 2. If you are just interested in the
SSRGA algorithm then you can use the ssrga.c
and ssrga.h source files.
- scatter-1.0.tar.gz (15 Dec 2016):
Older version.
- ssrga_matlab-2.0.tar.gz (15
Dec 2016): Matlab demonstration of SSRGA, including deriving the
SSRGA parameters from simulated aggregate structures. See the
README file in the package for further details. This code is in
the Public Domain: no copyright is asserted. Basically this means
you can do what you like with it.
- ssrga_matlab-1.0.tar.gz (12
July 2014): Older version based solely on the Hogan and Westbrook
(2014) paper. Running the
script compare_ice_scattering_models.m produces the
following images:
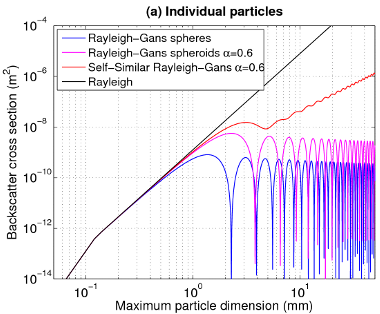 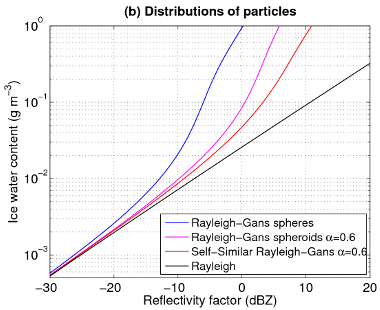
Comparison of the Self-Similar Rayleigh-Gans Approximation
(SSRG) with several other models for the 94-GHz backscatter
cross-section of aggregated ice particles and snowflakes. All
models assume the Brown and Francis (1995) mass-size relationship,
and two of them assume the particles to be horizontally aligned
with an aspect ratio of 0.6. The SSRGA model assumes the parameters
for aggregates of bullet rosettes reported
by Hogan
and Westbrook (2014) of κ=0.19, β=0.23 and
γ=5/3. The panels are (a) backscatter cross section of
ensembles of individual particles, all of the same size but with
different realizations of their internal structure, and (b) the
relationship between radar reflectivity factor and ice water
content for the Field et
al. (2005) size distributions.
Doesn't this contradict what you said in Hogan et al. (2012)?
Hogan et al. (2012)
claimed that homogeneous oblate spheroids ("soft spheroids") are a
good model for scattering by irregular ice particles at millimetre
wavelengths. While this is true for particles whose dimension in the
direction of propagation of radiation is smaller than the
wavelength, it is not true for larger particles. Note that the other
results of Hogan et al. (2012) are unaffected:
- The Brown & Francis (1995) mass-size relationship produces works
well in radar applications provided it is applied to the mean
of the maximum and minimum particle dimensions, rather than
the maximum particle dimension.
- Ice aggregates tend to have an aspect ratio of around 0.6.
- Soft spheroids work well for predicting radar parameters
(particularly reflectivity factor and differential reflectivity)
when the wavelength is longer than the size of the particle in the
direction of propagation.

|