Pulse Compression

Pulse compression, also known as pulse coding, is a signal processing technique designed to maximise the sensitivity and resolution of radar systems.

The sensitivity of a radar depends on the energy transmitted in the radar pulses. This can be expressed in terms of the average transmitted power- that is, the peak power multiplied by the transmitter duty cycle. Although the peak transmitter power may be as high as several hundred kilowatts, since most radars transmit very short pulses (typically a couple of microseconds long), the average transmitted power may be much less than 1% of this value. Clearly this is not an efficient use of the available transmitter power.

Transmitting longer pulses improves the radar's sensitivity by increasing the average transmitted power. However, simply lengthening the radar pulse has the effect of degrading the range resolution of the radar, since the radio pulse is just spread over a larger distance. A technique is needed for increasing the average power without compromising resolution.

The key to solving this problem is the realisation that the range resolution of a radar does not necessarily depend on the duration of the transmitted pulse; in fact, it depends on the bandwidth of the pulse. For a simple rectangular pulse, the bandwidth is just 1/T, where T is the pulse duration. However, by manipulating the amplitude and/or phase within the pulse, its bandwidth can be altered without changing its duration. In other words, the radar resolution can be changed independently of the average transmitted power. This manipulation of the transmitted pulse is known as pulse coding, or in some cases, pulse modulation.

Pulse compression refers to a family of techniques used to increase the bandwidth of radar pulses. In the radar receiver, these echo pulses are `compressed' in the time domain, resulting in a range resolution which is finer than that associated with an uncoded pulse. Many methods exist to achieve this, including binary phase coding, polyphase coding, frequency modulation, and frequency stepping. Methods involving changing the frequency of the transmitted pulse are often referred to as `chirp' pulses, in analogy to the sound of a frequency-modulated audio signal.

By far the most common pulse coding scheme used in meteorological radars is binary phase coding. This involves repeatedly flipping the phase of the radio frequency signal within the duration of the pulse, according to a binary code. The code is chosen so that, on decoding, range sigelobe effects are minimised. The most efficient binary codes using single code sequences are the Barker codes, which can have lengths of up to 13 bits. The decoding, or `compression' stage involves correlating the received signal with a replica of the transmitted code.

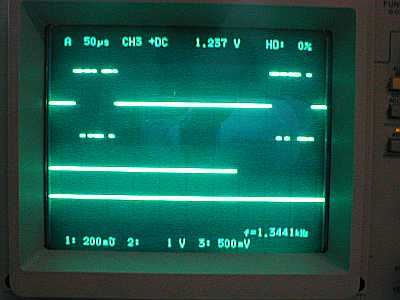
This top oscilloscope trace shows the two members of a complementary code pulse pair. This example shows a 16-bit long code. In an operational system, the inter-pulse period would be significantly longer than that shown here. The two lower traces are timing signals, and should be ignored.

The main disadvantage of pulse compression is the appearance of range sidelobes around the main signal peak, which have the effect of spreading out echoes from surrounding range gates, and introducing range ambiguities. This effect can be minimised by the use of complementary codes, which are carefully chosen pairs of codes whose range sidelobes cancel out under ideal conditions.

The effectiveness of a particular pulse code is often judged by its time-bandwidth product, BT, where B is the pulse bandwidth and T is the pulse duration. A simple uncoded pulse has BT=1, since B=1/T. A 13-bit Barker code, in contrast, has a time-bandwidth product of 13. This means that each radar pulse contains 13 times the energy of an uncoded pulse of the same resolution; or, equivalently, that the range resolution is 13 times finer than an uncoded pulse of the same duration.

Pulse Compression

Further reading

See also...